فیبوناچی چیست ؟
فیبوناچی / مفهومی بنیادین در ریاضیات و کاربردهای آن
در دنیای ریاضیات، اعداد فیبوناچی یکی از مهمترین و جذابترین مفاهیم هستند که در زمینههای مختلفی از جمله تحلیلهای مالی، علم زیستشناسی، معماری و هنر مورد استفاده قرار میگیرند. در این مقاله به معرفی دنباله فیبوناچی، نحوه ایجاد آن، و کاربردهای مختلف آن خواهیم پرداخت / اعداد فیبوناچی چیست ؟
دنباله فیبوناچی چیست؟
دنباله فیبوناچی یک سری از اعداد است که از دو عدد اولیه 0 و 1 شروع میشود و هر عدد بعدی از جمع دو عدد قبلی به دست میآید. به عبارت دیگر، دنباله فیبوناچی به صورت زیر تعریف میشود:
F(0)=0,F(1)=1,F(n)=F(n−1)+F(n−2)برایn≥2F(0) = 0, \quad F(1) = 1, \quad F(n) = F(n-1) + F(n-2) \quad \text{برای} \quad n \geq 2
این دنباله به شکل زیر شروع میشود:
0,1,1,2,3,5,8,13,21,34,55,89,…0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, \dots
تاریخچه فیبوناچی
دنباله فیبوناچی به نام ریاضیدان ایتالیایی، لئوناردو پیزانو (Leonardo Pisano) یا “فیبوناچی” نامگذاری شده است. او این دنباله را در کتاب معروف خود با عنوان Liber Abaci که در سال 1202 منتشر شد، معرفی کرد. در این کتاب، فیبوناچی از این دنباله برای مدلسازی رشد جمعیت خرگوشها استفاده کرد، اما پس از آن، این دنباله در بسیاری از زمینههای مختلف علمی و طبیعی کاربرد پیدا کرد / / اعداد فیبوناچی چیست ؟
پیشنهادی / پک فونت فارسی دیجی گرافیک
خواص جالب دنباله اعداد فیبوناچی
- نسبت طلایی (Golden Ratio): یکی از ویژگیهای جالب دنباله فیبوناچی، نسبت طلایی است که به آن “نسبت فیبوناچی” نیز گفته میشود. وقتی دو عدد متوالی از دنباله فیبوناچی را تقسیم کنید، نسبت حاصل به عدد ثابت حدوداً 1.618 نزدیک میشود. این نسبت به طور گسترده در هنر، معماری و طبیعت مشاهده میشود. نسبت طلایی را میتوان به صورت زیر تعریف کرد:ϕ=limn→∞F(n)F(n−1)≈1.618\phi = \lim_{n \to \infty} \frac{F(n)}{F(n-1)} \approx 1.618
- ظهور در طبیعت: دنباله فیبوناچی در بسیاری از اشکال طبیعی مانند گلها، برگها و صدفها دیده میشود. به طور مثال، تعداد گلبرگهای بسیاری از گلها و یا تعداد چرخشهای مارپیچی در صدفهای دریایی معمولاً از دنباله فیبوناچی پیروی میکنند.
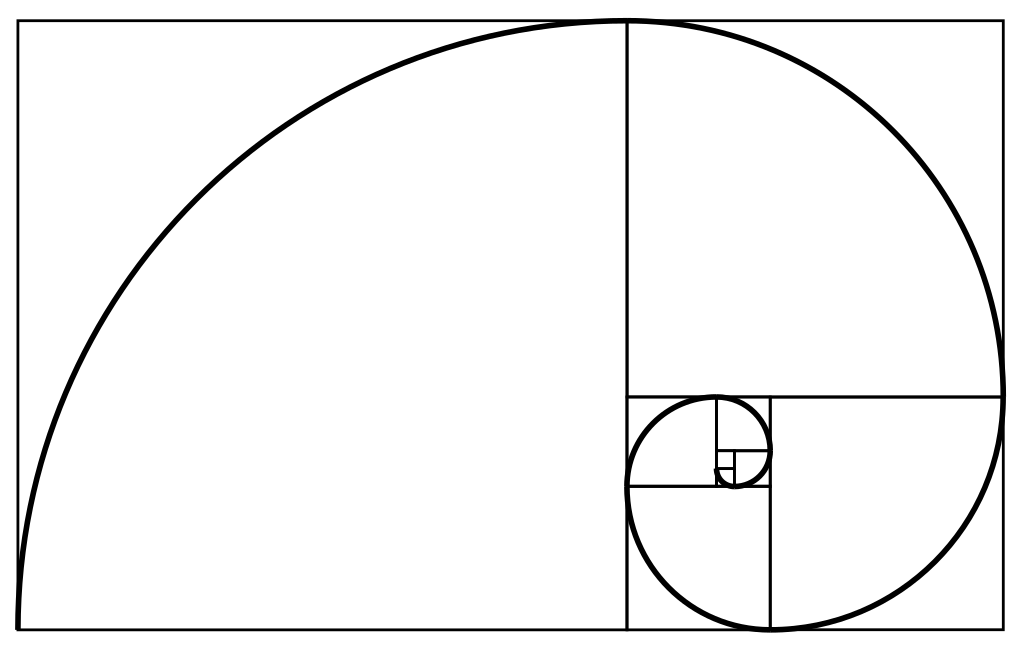
- ریاضیات و هندسه: دنباله فیبوناچی در هندسه نیز حضور دارد. یکی از کاربردهای آن در ساختار هندسی مارپیچها است که به نام مارپیچ فیبوناچی شناخته میشود. این مارپیچها به طور طبیعی در بسیاری از پدیدههای طبیعی مانند کهکشانها و گردابهای آب مشاهده میشوند / اعداد فیبوناچی
اگر به طبیعت دقت کنید به گلهای طبیعت ، تخمه های آفتاب گردان و بسیاری موارد دیگر، نظم خاصی در آنها می بینید. کل دنیا از نظم خاصی پیروی می کند.
دانشمندی به نام لئوناردو فیبوناچی که ایتالیائی بوده اعداد فیبوناچی را کشف می کند. از نظر این دانشمند همه چیز در دنیا و همه نسبت های اعداد از نظم خاصی پیروی می کند.
پیشنهادی / تبلیغات برای باشگاه بدنسازی
کاربردهای دنباله اعداد فیبوناچی چیست ؟
- تحلیل تکنیکال در بازارهای مالی: دنباله فیبوناچی به طور گسترده در تحلیل تکنیکال برای پیشبینی نوسانات قیمت در بازارهای مالی مانند بورس و ارزهای دیجیتال استفاده میشود. ابزارهای فیبوناچی مانند “سطوح اصلاحی فیبوناچی” و “فیبوناچی تایم زونها” برای شناسایی نقاط بازگشت و روندهای قیمتی مورد استفاده قرار میگیرند. این ابزارها به تحلیلگران کمک میکنند تا به سطوح مهم قیمتی مانند مقاومت و حمایت در بازار پی ببرند / چاپ کارت ویزیت
- علوم زیستی: در علم زیستشناسی، دنباله فیبوناچی به طور چشمگیری در ساختارهای مختلف بدن موجودات زنده مشاهده میشود. به عنوان مثال، در رشد گیاهان، الگوی چیدمان برگها و گلها به گونهای است که بتوانند بیشترین نور را جذب کنند. این الگوها اغلب با استفاده از دنباله فیبوناچی مدلسازی میشوند.
- هنر و معماری: دنباله فیبوناچی و نسبت طلایی در هنر و معماری برای ایجاد تناسبات و تعادل استفاده میشوند. به عنوان مثال، بسیاری از نقاشیها و ساختمانهای مشهور مانند پارتنون در یونان به گونهای طراحی شدهاند که نسبتهای آنها مطابق با نسبت طلایی باشد. این اصول به طراحان کمک میکند تا اثرهایی زیبا و متوازن خلق کنند / اعداد فیبوناچی
- الگوریتمها و علوم کامپیوتر: در برنامهنویسی و الگوریتمها، دنباله فیبوناچی برای حل مسائلی مانند تقسیم و غلبه، جستجو و مرتبسازی استفاده میشود. الگوریتمهای مختلفی وجود دارند که برای محاسبه اعداد فیبوناچی بهینه شدهاند.
- فیزیک و مهندسی: در فیزیک و مهندسی، دنباله فیبوناچی برای مدلسازی سیستمهای دینامیکی، تشخیص الگوها و حل مسائل پیچیده به کار میرود. در برخی از مسائل فیزیکی، مانند تحلیل ارتعاشات و مکانیک، ممکن است مدلهای مبتنی بر دنباله فیبوناچی برای سادهسازی محاسبات استفاده شوند.
دنباله فیبوناچی نه تنها در ریاضیات، بلکه در بسیاری از زمینههای دیگر مانند طبیعت، هنر، معماری و حتی تحلیلهای مالی کاربرد دارد. این دنباله با ویژگیهای خاص خود، مانند نسبت طلایی، توانسته است توجه بسیاری از دانشمندان، هنرمندان و تحلیلگران را جلب کند. با درک بهتر این مفاهیم و کاربردهای آن، میتوانیم به بهرهبرداری بهینه از آنها در حوزههای مختلف بپردازیم / اعداد فیبوناچی








دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.